Adaptive Array Processing

Adaptive Array Processing including LMS, and LS algorithms

View the Project on GitHub

 

Conventional Beamformer

Contents

Background

Conventional Beamformer

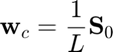
Weight vector: $$\textbf{w}_c=\frac{1}{L}\textbf{S}_0$

Correlation Matrix

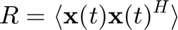
$$R = \langle\textbf{x}(t)\textbf{x}(t)^H\rangle$

Array output

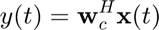
$$y(t)=\textbf{w}_c^H\textbf{x}(t)$

Simulation Algorithm

  1. Generate signal for L element array
  2. Use Coventional Beamformer weight vector
  3. Calculate the array output y
  4. Calculate output SNR
  5. Calculate array Gain

Simulation Parameters

  • Number of array elements: $$L=16$
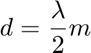
  • Element spacing: $$d=\frac{\lambda}{2}m$
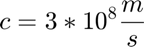
  • Propagation speed: $$c=3*10^8\frac{m}{s}$
  • Signal to Noise Ratio: $$SNR=[3, 10]dB$
  • Signal power: $$ps=1$
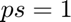
  • Noise power: $$\sigma_n^2=[0.5, 0.1]$
  • Number of samples: $$N=[10,100]$
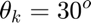
  • Source direction: $$\theta_k=30^o$
  • Steering Vector in the Look direction: $$\textbf{S}_0=[exp({j2{\pi}f_0{\tau}_l}),\ldots,exp({j2{\pi}f_0{\tau}_L})]^T$

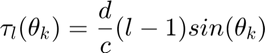
Where $$\tau_l(\theta_k)=\frac{d}{c}(l-1)sin(\theta_k)$

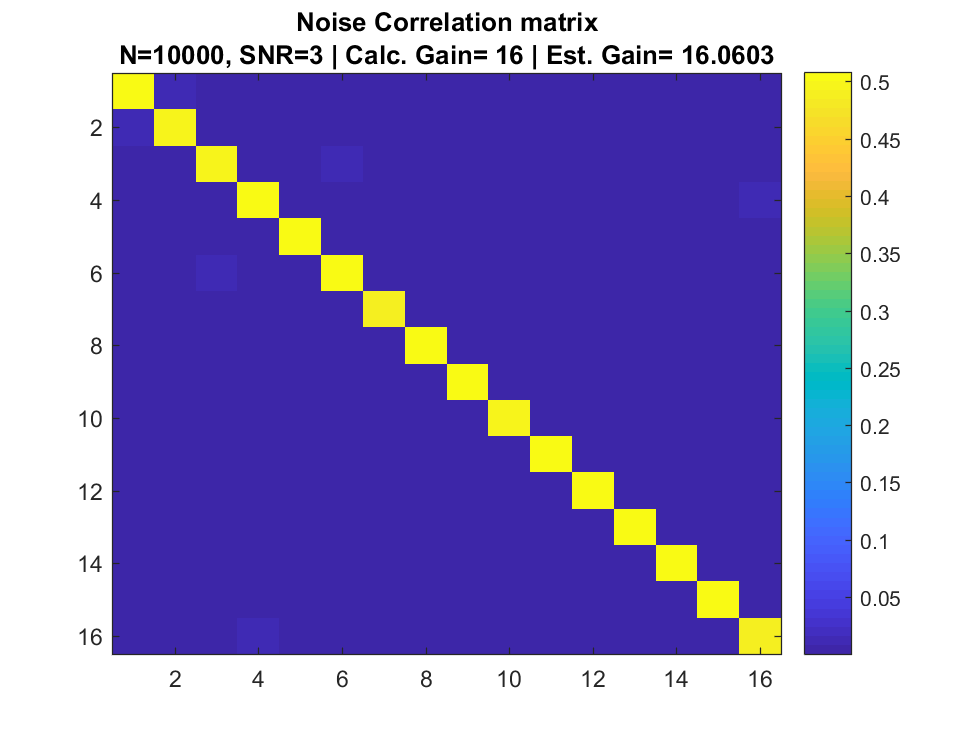
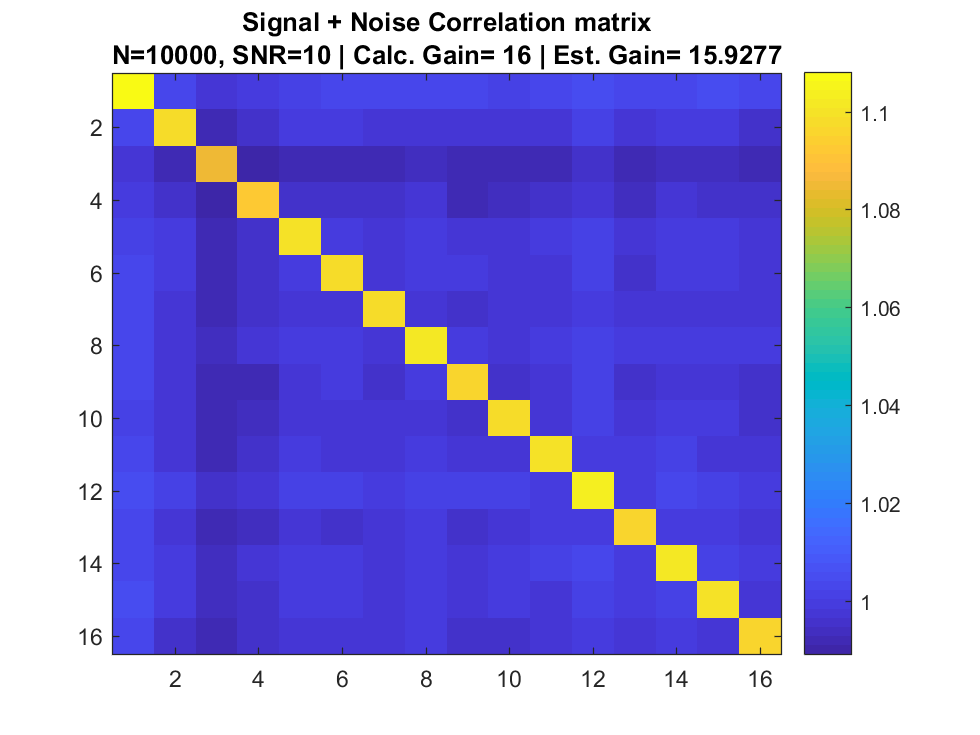
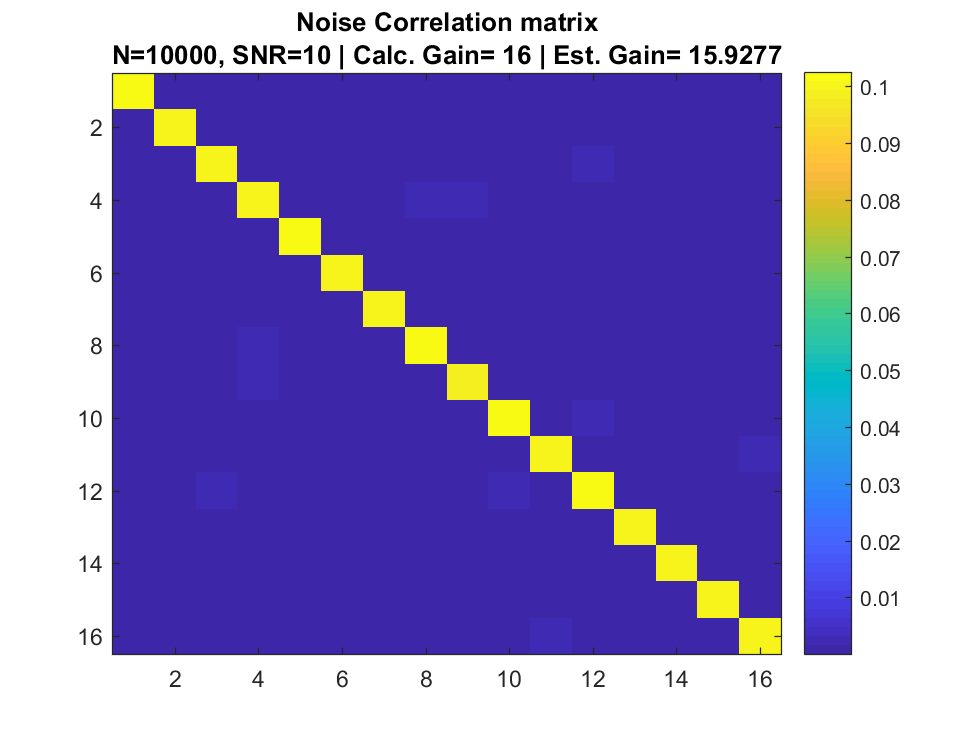
Signal + Noise Only

Array input

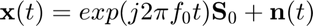
$$\textbf{x}(t)=exp({j2{\pi}f_0t})\textbf{S}_0+\textbf{n}(t)$$

Correlation Matrix

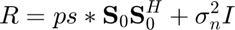
$$R=ps*\textbf{S}_0\textbf{S}_0^H+{\sigma}_n^2{I}$$

Signal to Noise Ratio

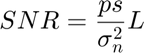
$$SNR=\frac{ps}{\sigma_n^2}L$$

Array Gain

$$G=L$$

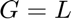
Simulation

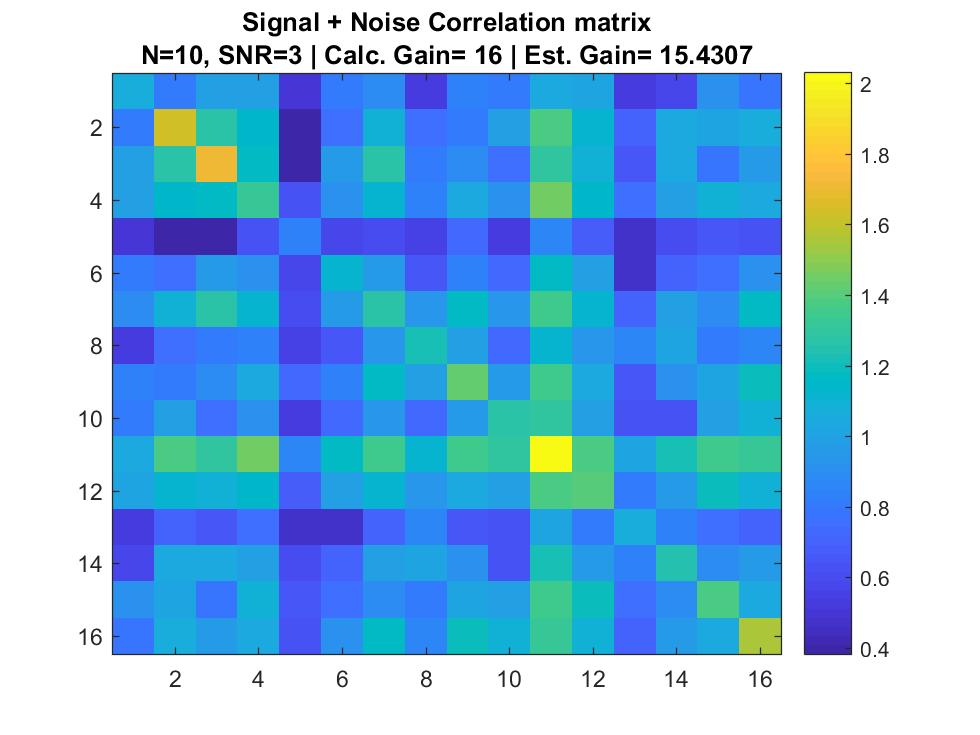
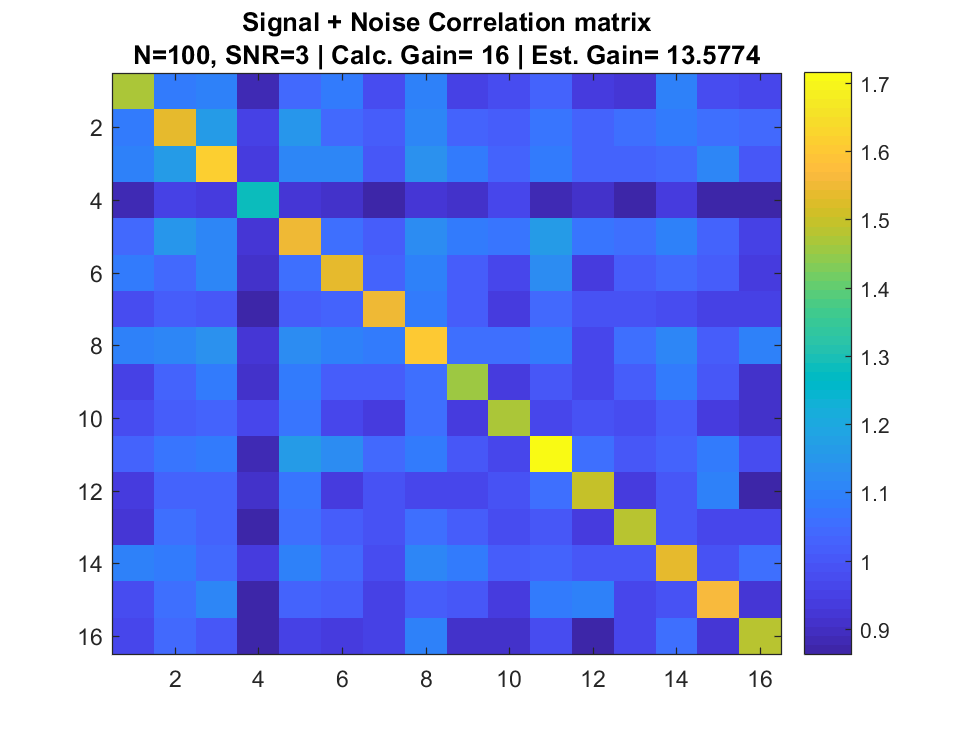
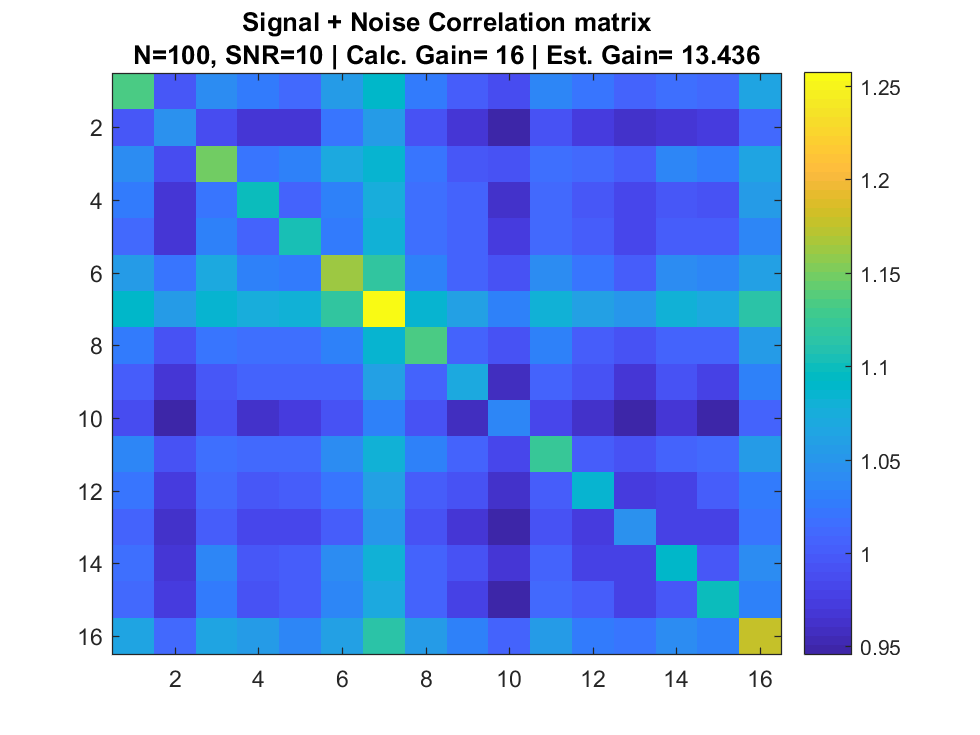
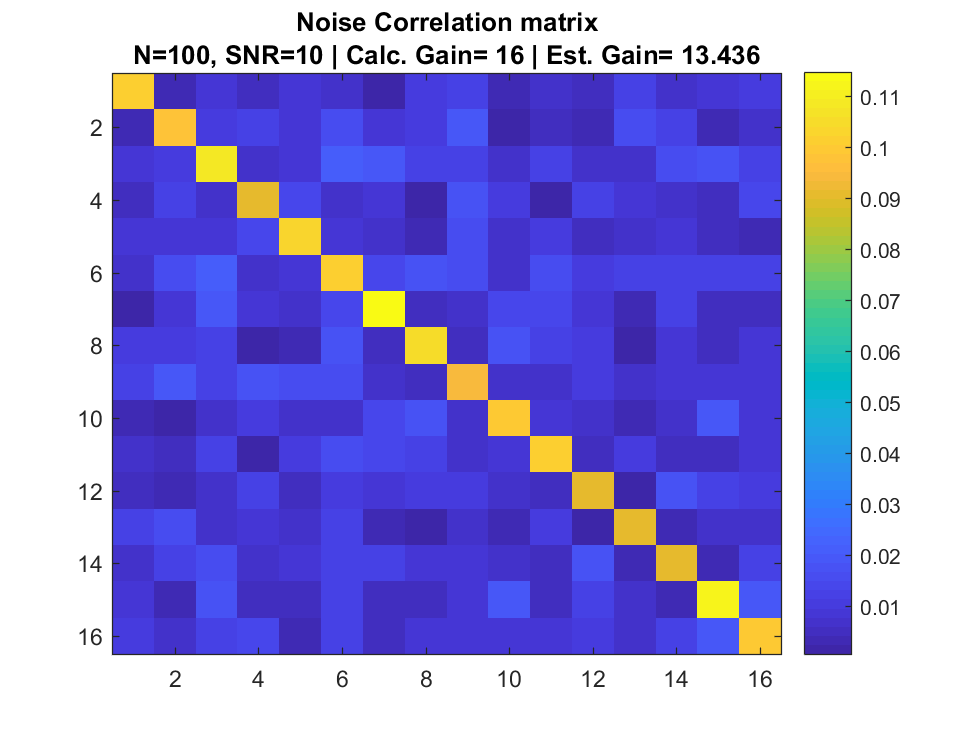
Signal + Interference + Noise

Array input

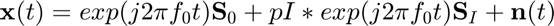
$$\textbf{x}(t)=exp({j2{\pi}f_0t})\textbf{S}_0+pI*exp({j2{\pi}f_0t})\textbf{S}_I+\textbf{n}(t)$$

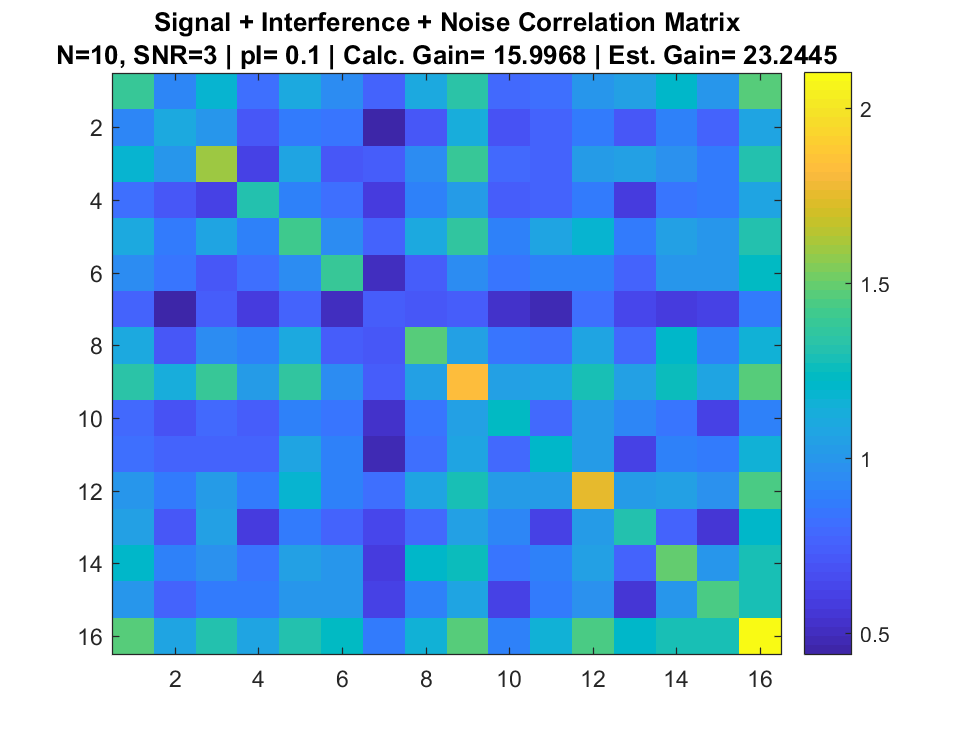
Correlation Matrix

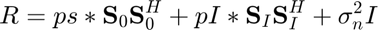
$$R=ps*\textbf{S}_0\textbf{S}_0^H+pI*\textbf{S}_I\textbf{S}_I^H+{\sigma}_n^2{I}$$

Signal to Noise Ratio

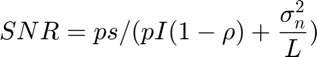
$$SNR=ps/(pI(1-\rho)+\frac{\sigma_n^2}{L})$$

Array Gain

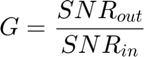
$$G=\frac{SNR_{out}}{SNR_{in}}$$

Simulation

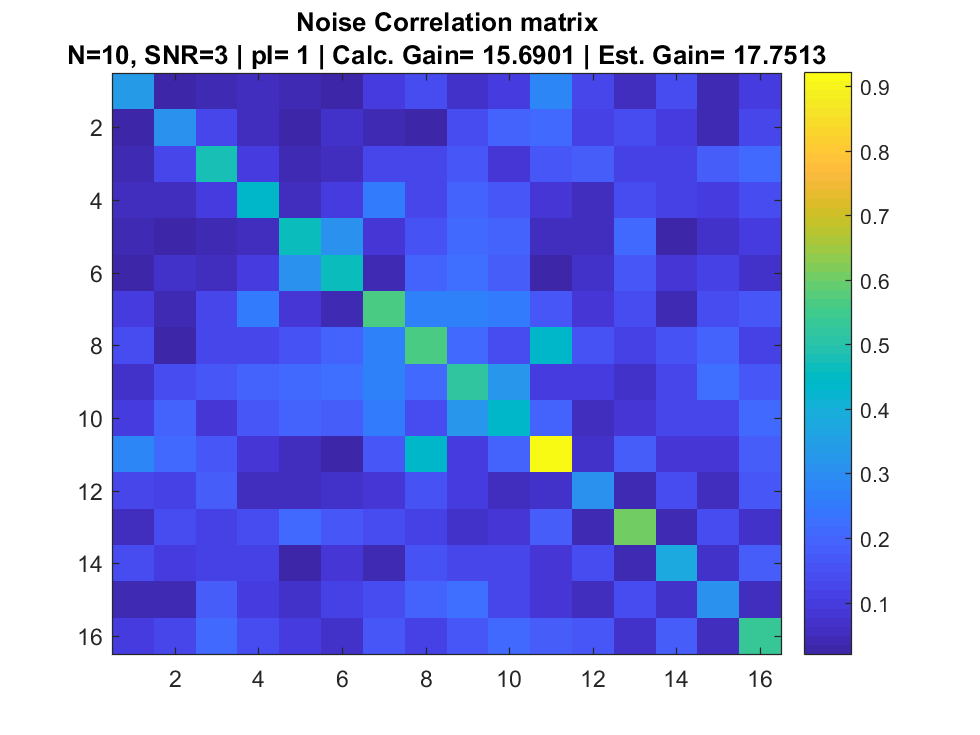
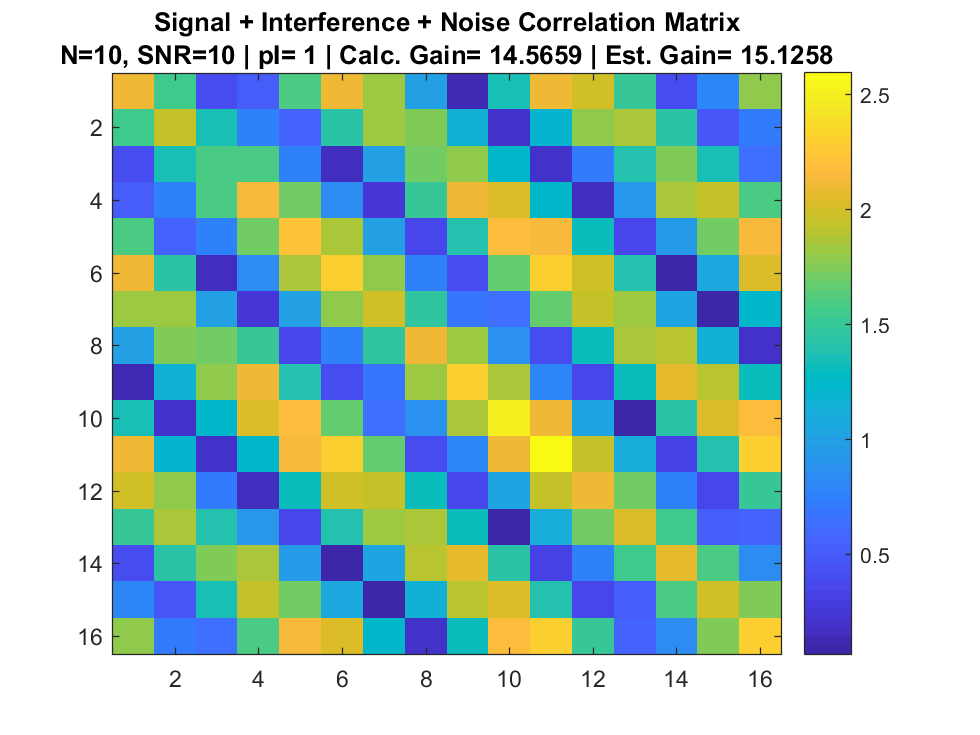
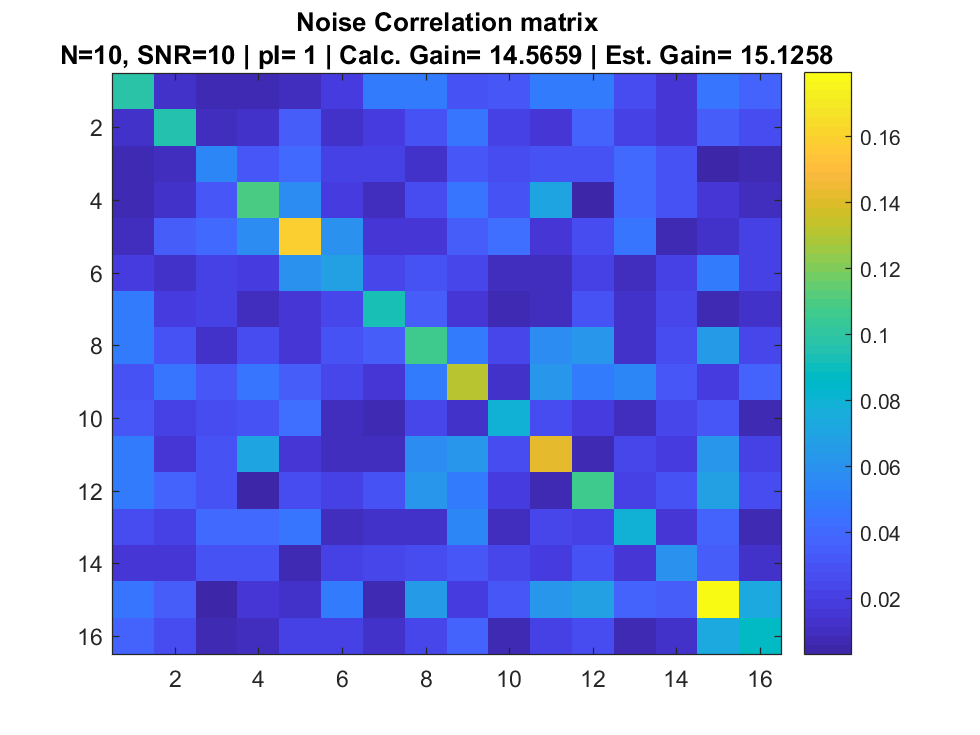
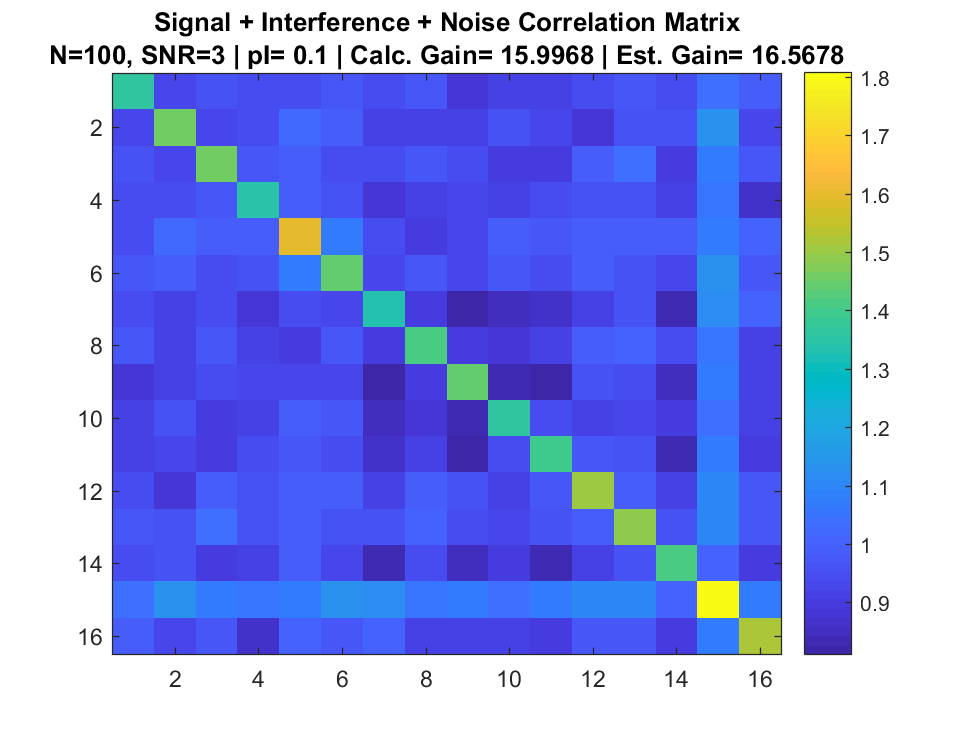
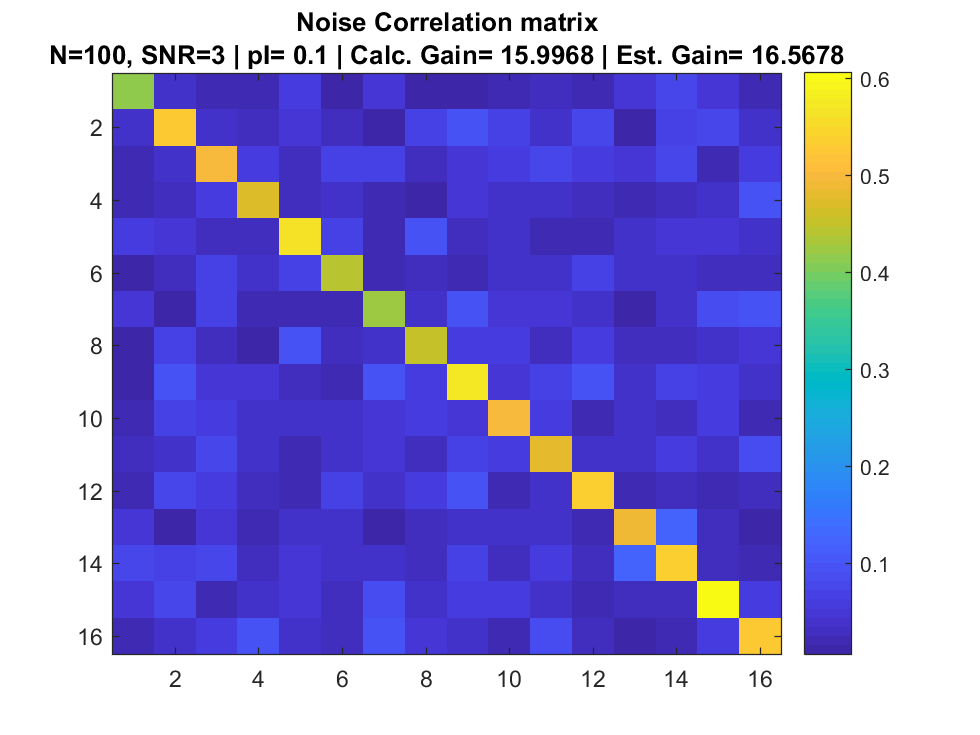
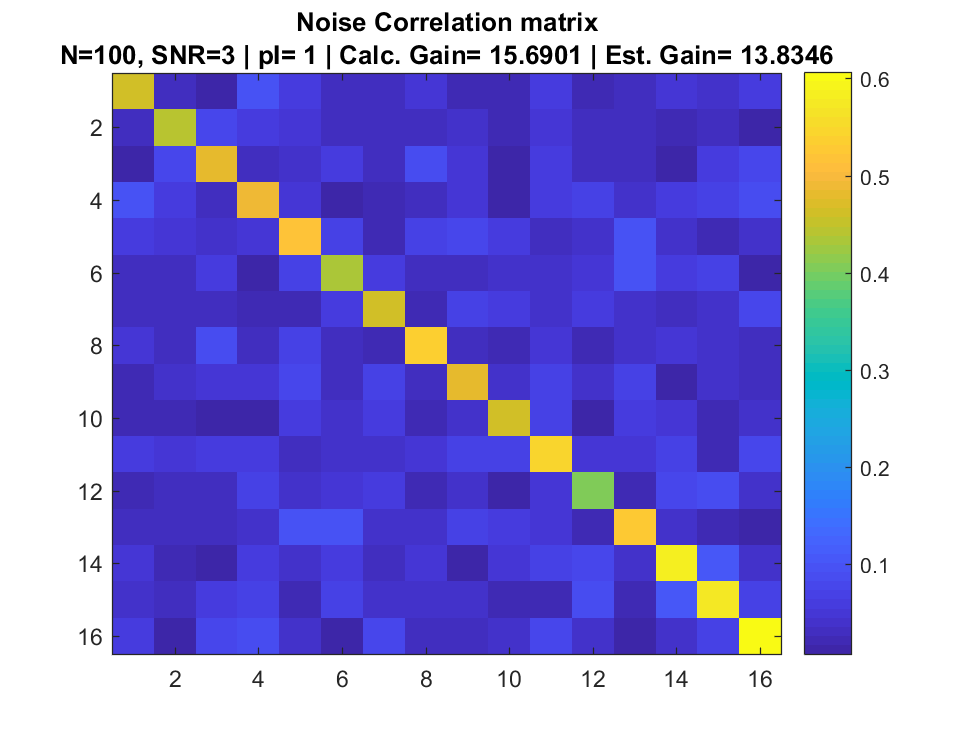
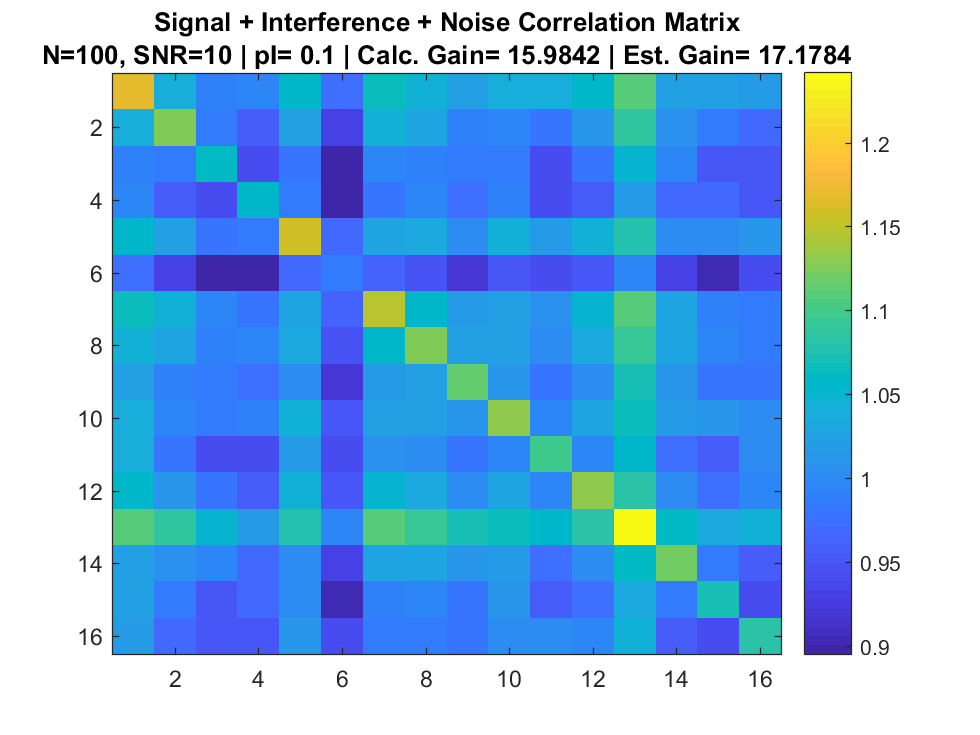
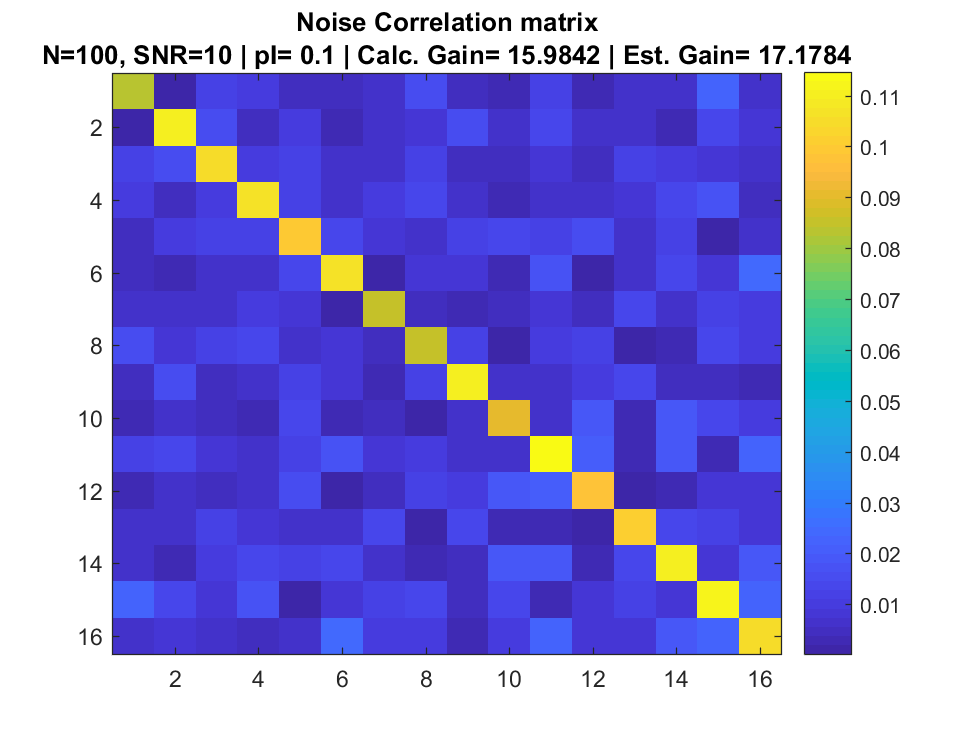
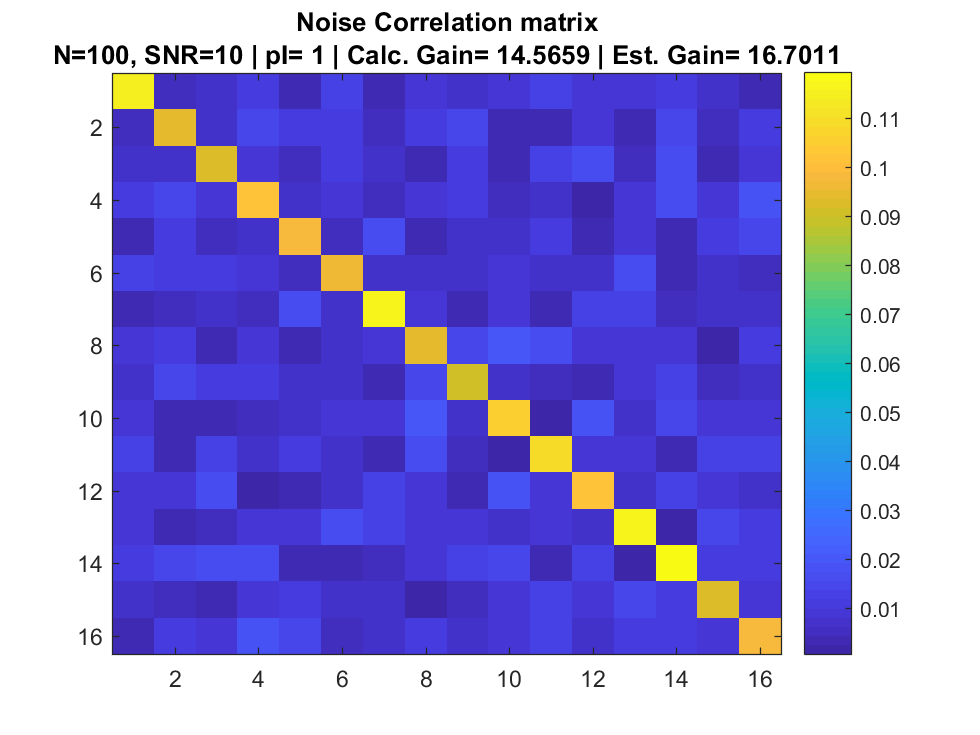
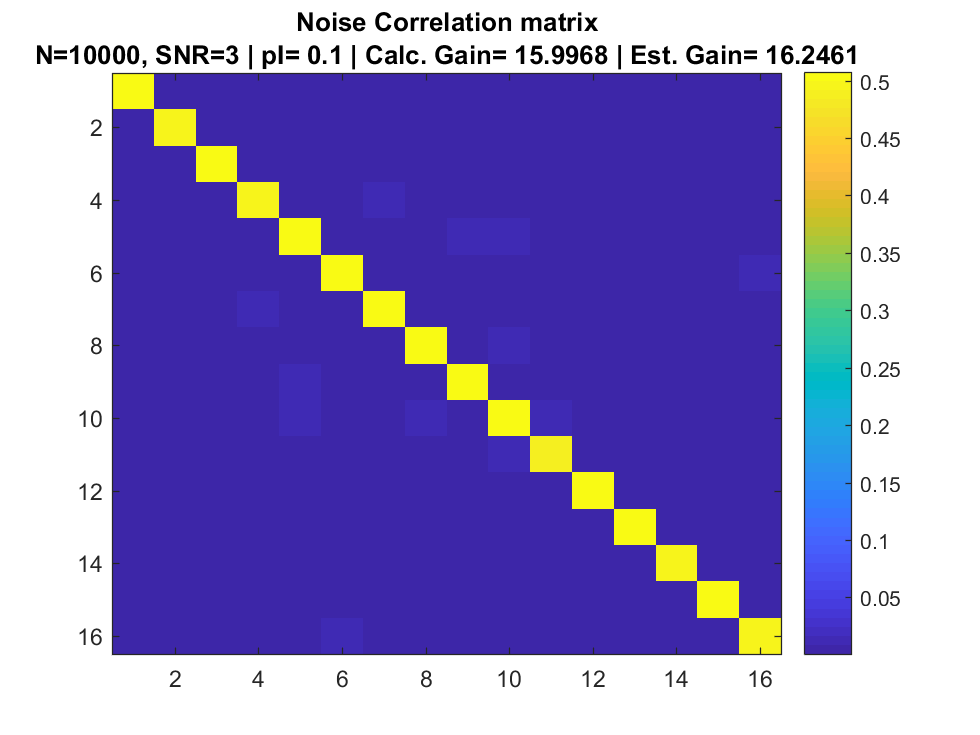
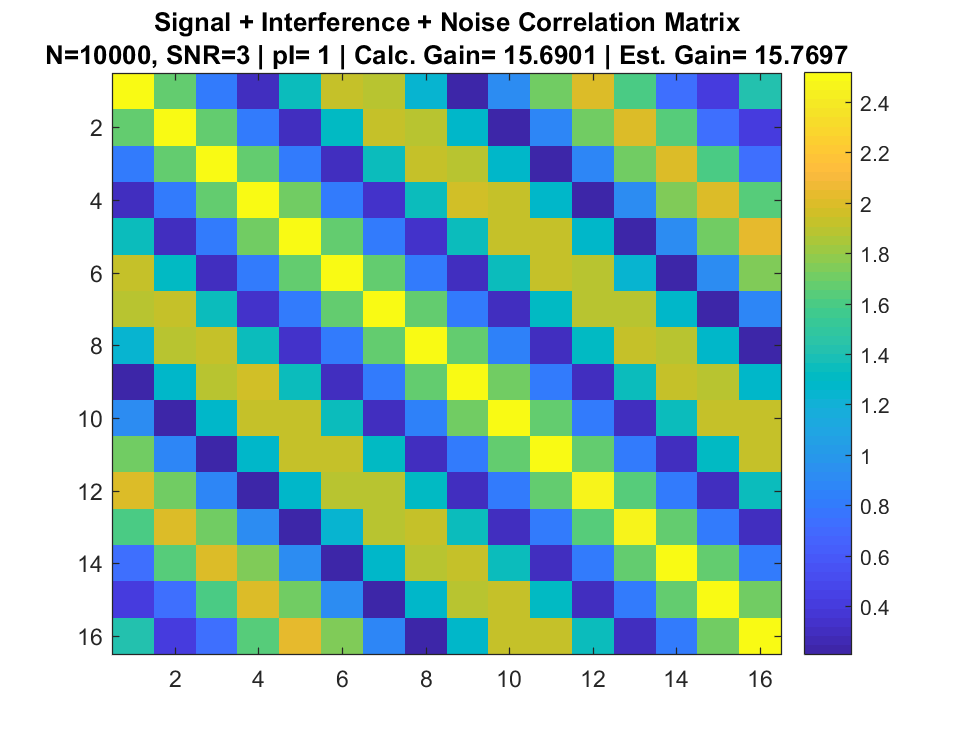
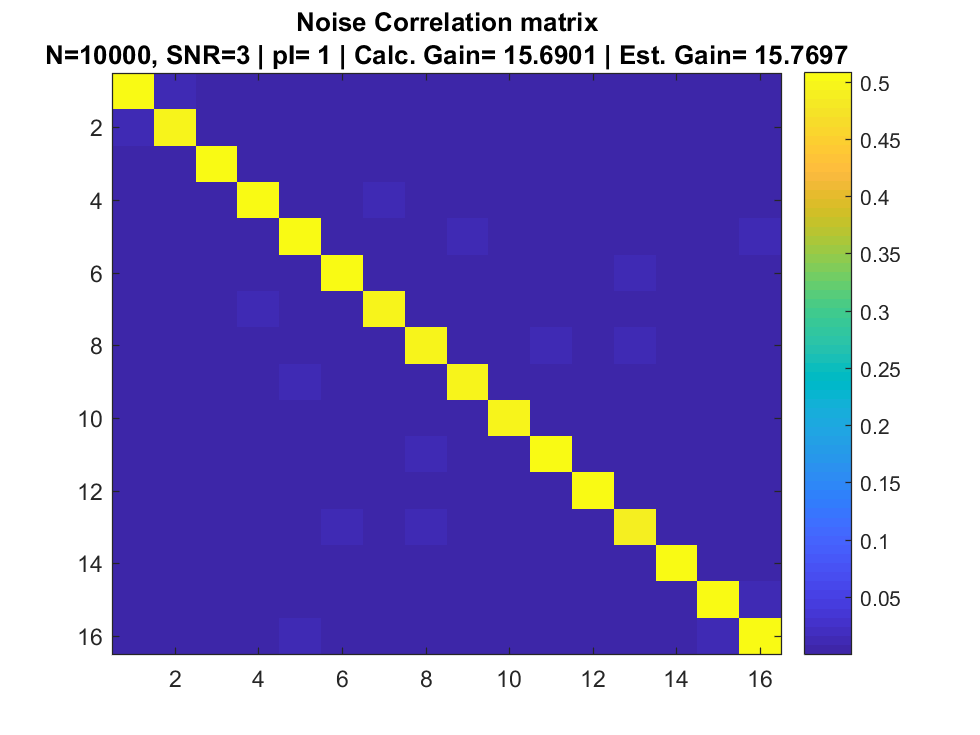
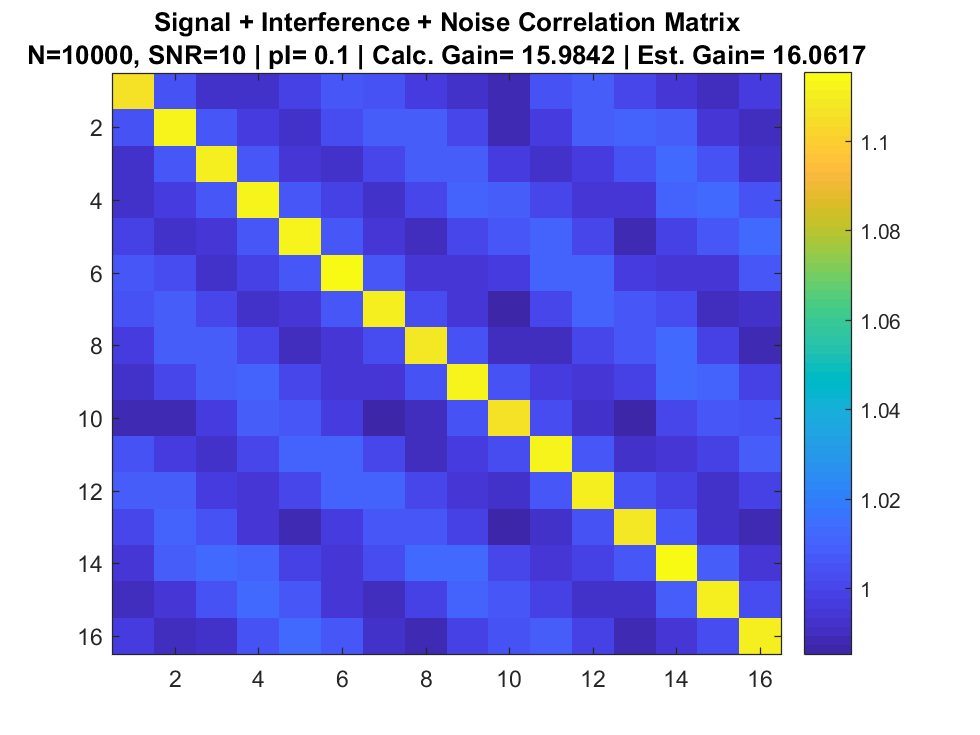
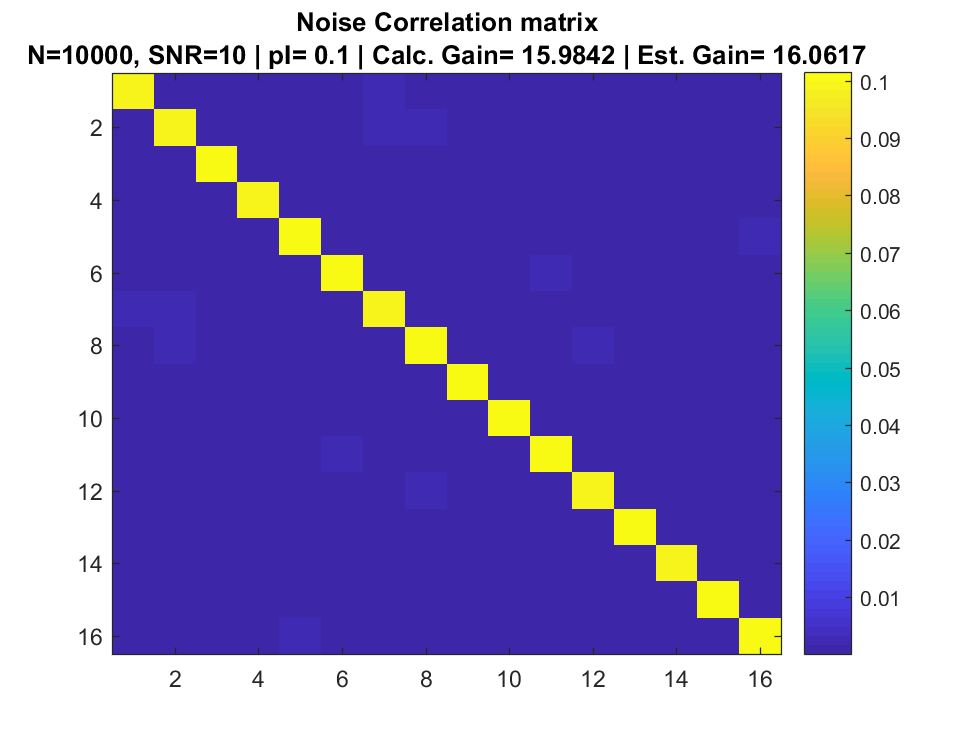
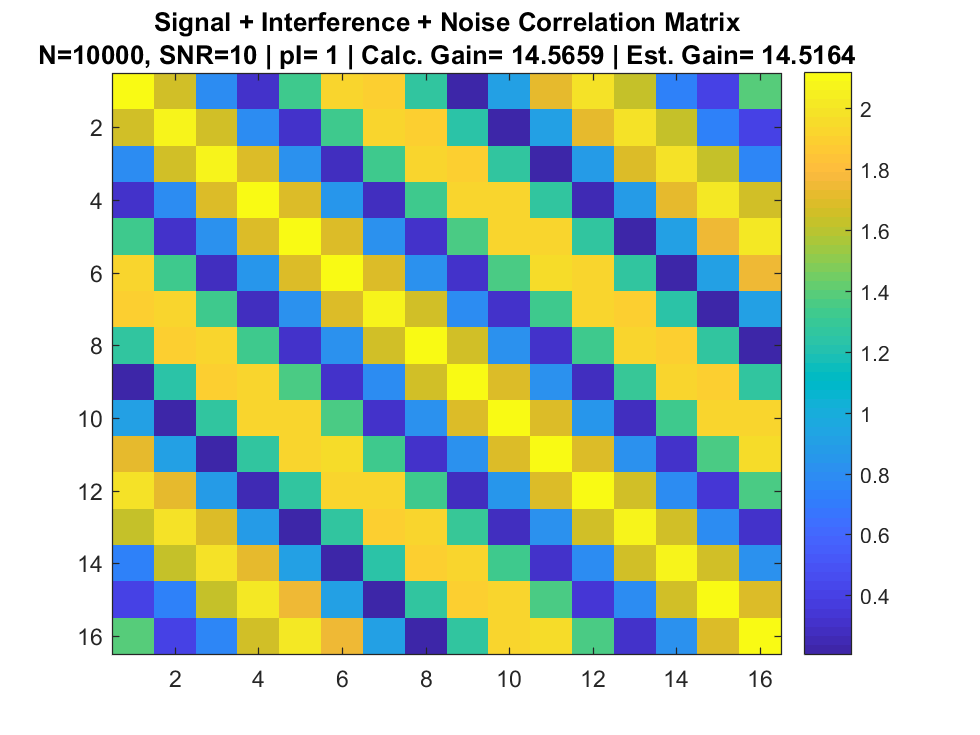
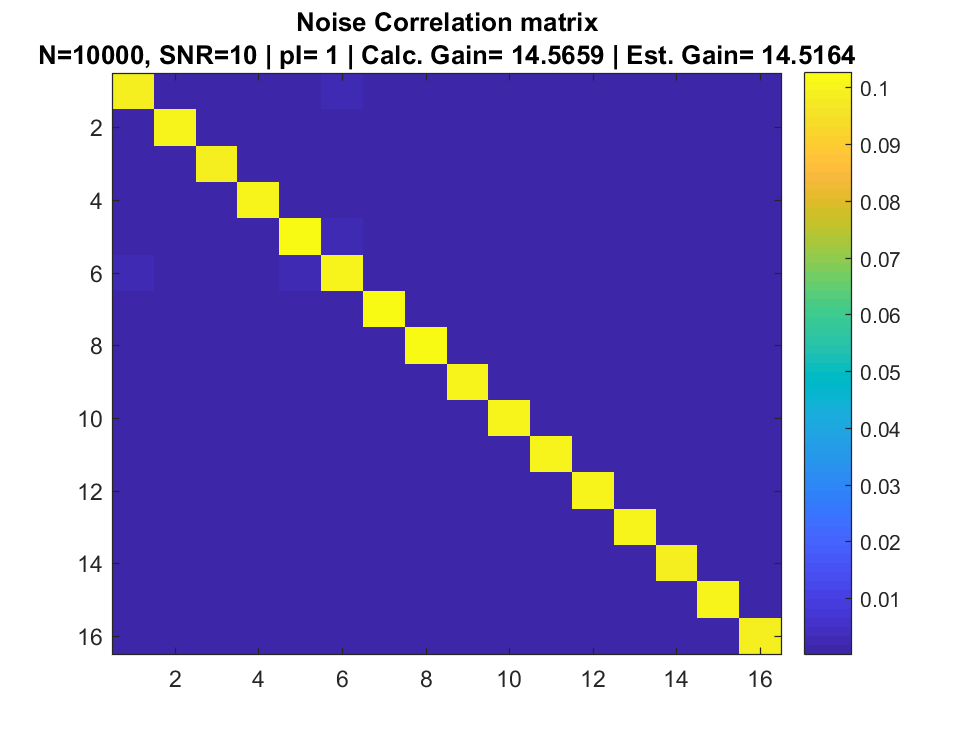
References

[1] L. Godara, Smart antennas. Boca Raton: CRC Press, 2004.


Published with MATLAB® R2017a